Introduction

L'une des premieres techniques de synthèse sonore est la synthèse soustractive. Cette technique de synthèse repose sur la génération d'un signal riche en fréquence que l'on sculpte via un filtre dont les paramètres peuvent être contrôlés (fréquence de coupure, résonance, etc). Certains filtres analogiques sont devenus mythiques comme le filtre des synthés Moog ou le filtre passe-bas de la TB303.

Dans notre projet, nous allons implémenter une version numérique d'un State Variable Filter (SVF) analogique. Ce filtre permet de contrôler simplement la fréquence de coupure et le paramètre Q.

Filtre SVF

La structure d'un SVF numérique est présenté sur la figure suivante. Cette structure de filtre présente l'avantage de pouvoir commuter facilement entre 3 types de filtres (passe-bas, passe-haut, passe-bande).

Structure du filtre analogique

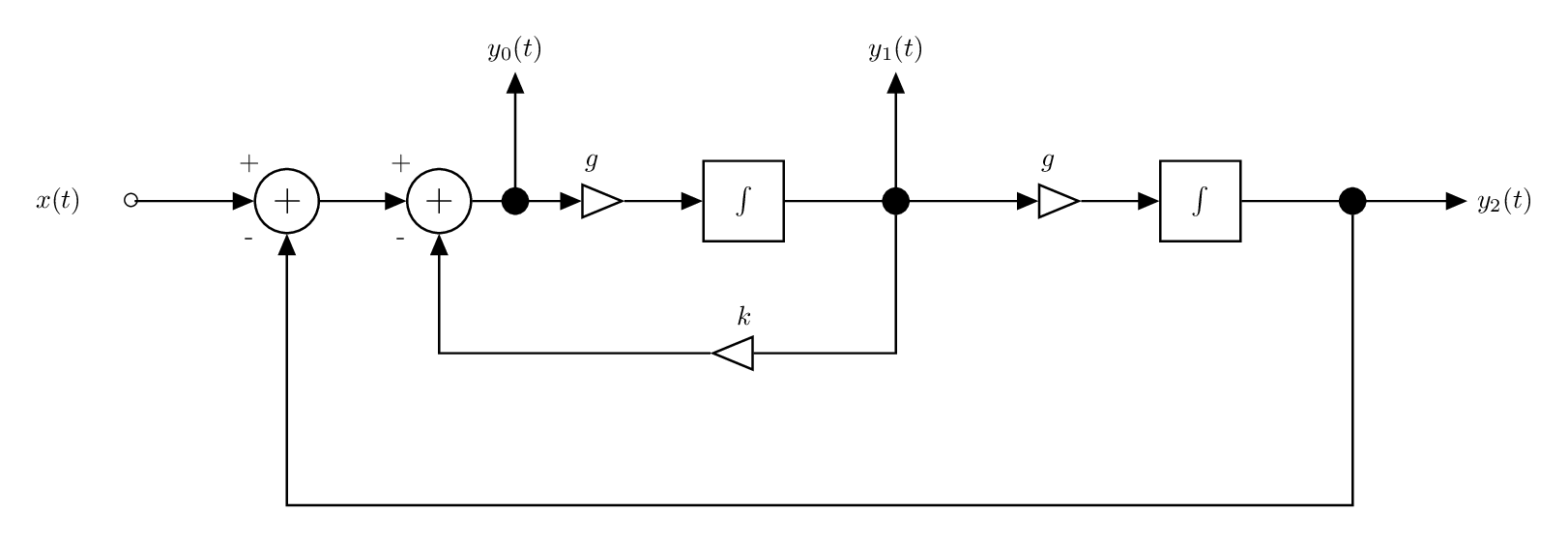
En fonction de la sortie $y(t)$ sélectionnée, il est possible d'obtenir différents filtres.

• Passe-Bas: $y(t)=y_2(t)$,
• Passe-Bande: $y(t)=y_1(t)$,
• Passe-Haut: $y(t)=y_0(t)$.

Numérisation

Pour numériser le filtre analogique, une approche possible consiste à approximer l'intégration par la méthode des trapèzes.

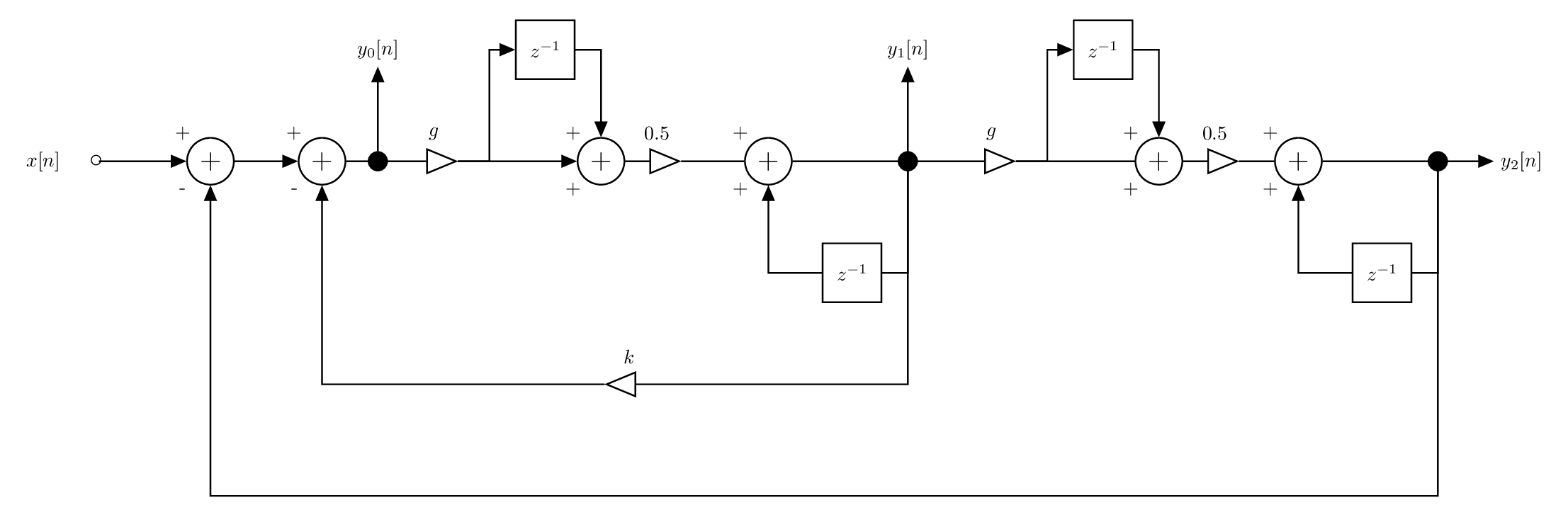
Calibration des coefficients

Il est possible de calibrer les coefficients du filtre $g$ et $k$ à partir de la fréquence de coupure du filtre $f_c$ et du paramètre $Q$ (lié au facteur de qualité) via les relations :

$$\begin{array}{rl}g& =\tan (\pi f_c/f_s)\\ k& =1-0.95Q;\end{array}$$

Mise en équation

A partir du schéma-bloc et en substituant $g$ par $2g$ pour simplifier les calculs, il est possible d'obtenir le système suivant:

$$\begin{array}{rl}{y}_0[n]& =x[n]-k{y}_1[n]-y_2[n]\\ y_1[n]& =y_1[n-1]+g(y_0[n]+y_0[n-1])\\ y_2[n]& =y_2[n-1]+g(y_1[n]+y_1[n-1])\end{array}$$

Equations d'état

Les équations d'état s'obtiennent en écrivant les équations précédentes sous forme matricielle. Après quelques manipulations matricielles (réalisées numériquement), il est possible d'établir que :

$$\left[\begin{array}{c}{y}_0[n]\\ y_1[n]\\ y_2[n]\end{array}\right]=c_0\left[\begin{array}{ccc}-g(g+k)& -(2g+k)& -1\\ g& 1-g^2& -g\\ g^2& g(gk+2)& gk+1\end{array}\right]\left[\begin{array}{c}{y}_0[n-1]\\ v_1[n-1]\\ v_2[n-1]\end{array}\right]+c_0\left[\begin{array}{c}1\\ g\\ g^2\end{array}\right]x[n]$$

où

$$c_0=\frac{1}{1+g(g+k)}$$

Filtre optimisé

Il est possible d'adapter la structure du filtre numérique précédent afin d'obtenir des coefficients moins sensibles aux erreurs numériques (filtre d'Andrew Simper). L'idée est de remplacer dans le vecteur d'état $y_0[n]$ par $x[n]$. En utilisant cette approche, les équations d'états modifiées sont alors données sous la forme matricielle suivante :

$$\left[\begin{array}{c}{y}_0[n]\\ y_1[n]\\ y_2[n]\end{array}\right]=\left[\begin{array}{ccc}0& 0& 0\\ c_1& 1-2(g+k)c_1& -2c_1\\ g{c}_1& 2c_1& 1-2g{c}_1\end{array}\right]\left[\begin{array}{c}{y}_0[n-1]\\ y_1[n-1]\\ y_2[n-1]\end{array}\right]+\left[\begin{array}{c}1\\ c_1\\ g{c}_1\end{array}\right]x[n]$$

où:

$$c_1=\frac{g}{1+g(g+k)}$$

En fonction de la sortie $y[n]$ sélectionnée, il est possible d'obtenir différents filtres.

• Passe-Bas: $y[n]=y_2[n]$,
• Passe-Bande: $y[n]=y_1[n]$,
• Passe-Haut: $y[n]=y_0[n]-k{y}_1[n]-y_2[n]$.

Analyse Fréquentielle

Les librairies Numpy/Scipy de Python permettent d'obtenir la réponse fréquentielle du filtre facilement.

import numpy as np
from scipy.signal import dlti, dfreqresp
import matplotlib.pyplot as plt

# Define the parameters
Fs = 44100
fc = 100
Q = 0.5
g = np.tan(np.pi*fc/Fs)
k = 1-0.99*Q
c1 = g/(1+g*(g+k))

# Create the discrete-time linear system
A = np.array([
    [0, 0, 0],
    [c1, 1 - 2 * (g + k) * c1, -2 * c1],
    [g * c1, 2 * c1, 1 - 2 * g * c1]
])

B = np.array([
    [1],
    [c1],
    [g * c1]
])

index_output = 2
C = np.eye(3)  # Output matrix to output the full state
D = np.zeros((3, 1))  # No direct transmission from input to output
system = dlti(A, B, C[index_output, :], D[index_output, :], dt=1/Fs)

# compute frequency response
w, h = dfreqresp(system)
f = w*Fs/(2*np.pi)
magnitude = np.abs(h)
phase = np.unwrap(np.angle(h))

# Plotting
plt.figure()
plt.subplot(2, 1, 1)
plt.loglog(f, magnitude)
plt.ylim([0.001, 10*np.max(magnitude)])
plt.title('Magnitude Response')
plt.xlabel('Frequency (rad/sample)')
plt.ylabel('Magnitude')

plt.subplot(2, 1, 2)
plt.semilogx(f, phase)
plt.title('Phase Response')
plt.xlabel('Frequency (rad/sample)')
plt.ylabel('Phase (radians)')

plt.tight_layout()
plt.show()

References

• https://cytomic.com/files/dsp/SvfLinearTrapOptimised.pdf