Synthèse sinusoïdale

La synthèse d'une onde sinusoïdale est fondamentale en synthèse sonore, car elle constitue la brique élémentaire des sons plus complexes. D'une part, en additionnant plusieurs sinusoïdes, il est théoriquement possible de synthétiser n'importe quel signal périodique (décomposition en série de Fourier). D'autre part, les oscillateurs sinusoïdaux sont souvent utilisés comme composants de base en synthèse FM pour générer des timbres très complexes. Cette dualité rend la maîtrise de la synthèse sinusoïdale essentielle pour explorer toute la gamme des possibilités sonores offertes par les techniques modernes de synthèse.

Dans cette section, nous explorons différentes méthodes pour générer une sinusoïde pure à fréquence variable, avec une attention particulière portée sur la réduction de la complexité calculatoire.

INFO

Dans cette partie, ne raccordez pas le contrôleur MIDI à la carte.

Modèle de signal

Le modèle de signal d'une sinusoïde numérique est donnée par:

$$y[n]=a\sin (2\pi n{f}_0/f_s+{\phi }_0)$$

où :

• $a$ est l'amplitude crête du signal,
• ${\phi }_0$ est le déphasage initial,
• $f_0$ est la fréquence de la sinusoïde,
• $f_s$ correspond à la fréquence d'échantillonnage.

La figure suivante présente l'allure d'une sinusoïde échantillonnée à $f_s=44.1$ kHz.

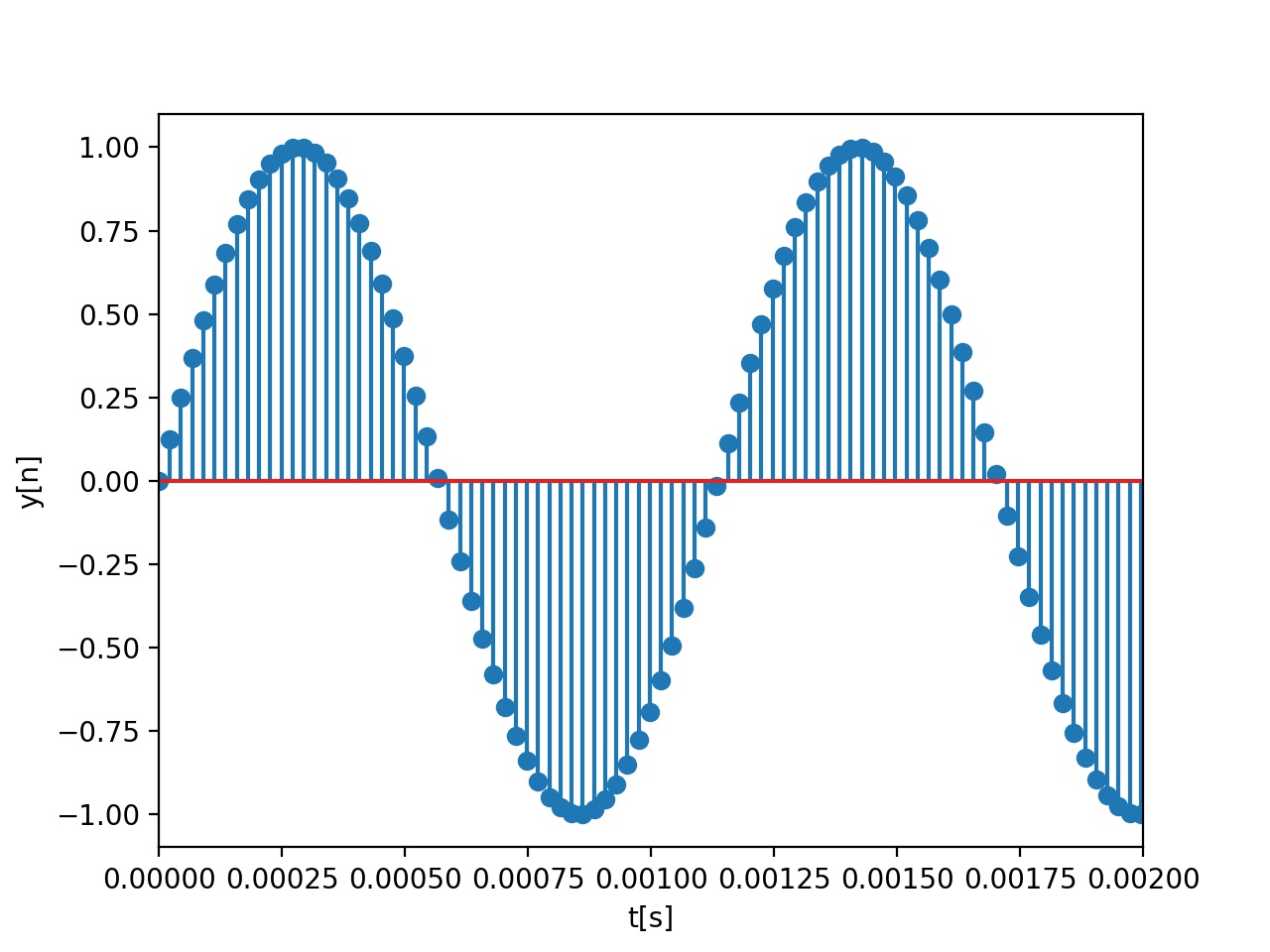
Implémentation 1 : Utilisation de la bibliothèque math.h

Manipulation 1

En utilisant la bibliothèque math.h, générez une sinusoïde de fréquence $f_0=220$ Hz et d'amplitude crête $a=1$. Attention à bien gérer la continuité de la phase entre 2 buffer audio.

Implémentation 2 : Gestion de la continuité de phase

La technique précédente peut être limitée par la nécessité de gérer la continuité de la phase entre deux buffers audio. Une méthode plus efficace consiste à utiliser le modèle suivant :

$$\begin{array}{rl}\varphi [n]& =\varphi [n-1]+\phi \\ y[n]& =a\sin (\varphi [n])\end{array}$$

où :

• $\varphi [n]$ représente la phase instantanée du signal ($\varphi [n]={\phi }_0$)
• $\phi =2\pi f_0/f_s$ est l'incrément de phase entre deux échantillons consécutifs.

Manipulation 2

Générez une sinusoïde de fréquence $f_0=220$ Hz et d'amplitude crête $a=0.9$ en appliquant cette méthode.

Implémentation 3: Optimisation du calcul

La technique précédente repose sur l'utilisation de la fonction sin. L'utilisation de cette fonction alourdit considérablement la charge calculatoire du microcontroleur. Cette surcharge en calculs peut provoquer des artefacts audios. Pour réduire la charge calculatoire, il est possible d'exploiter les propriétés trigonométriques des fonctions $\sin ()$ et $\cos ()$.

Notons $\cos (a)$ et $\sin (a)$ la composante directe (I) et en quadrature (Q) du signal. En utilisant la décomposition de $\cos (a+b)$ et $\sin (a+b)$, il est possible de calculer la composante directe (I) et en quadrature (Q) après un incrément de phase $b$ à partir de combinaisons linéaires :

$$\begin{array}{rl}\cos (a+b)& =\cos (a)\cos (b)-\sin (a)\sin (b)\\ \sin (a+b)& =\cos (a)\sin (b)+\sin (a)\cos (b)\end{array}$$

Bien que cette decomposition fasse apparaitre plusieurs fonctions trigonométriques, son avantage réside dans le fait que les termes $\cos (b)$ et $\sin (b)$ peuvent être calculés qu'une seule fois lorsque la fréquence de l'oscillateur est fixe. Dans ce contexte, il est possible de générer efficacement une sinusoide de la manière suivante :

$$\left[\begin{array}{c}{y}_I[n]\\ y_Q[n]\end{array}\right]=\left[\begin{array}{cc}\cos (\phi )& -\sin (\phi )\\ \sin (\phi )& \cos (\phi )\end{array}\right]\left[\begin{array}{c}{y}_I[n-1]\\ y_Q[n-1]\end{array}\right]$$$$y[n]=y_Q[n]$$

où

• $y_I[n]=\cos (\varphi [n])$ représente la composante directe,
• $y_Q[n]=\sin (\varphi [n])$ représente la composante en quadrature.

Manipulation 3

Générez une sinusoïde de fréquence $f_0=220$ Hz et d'amplitude crête $a=0.9$ en appliquant cette méthode et en utilisant les initialisations y_I[0]=0 et y_Q[0]=1.

Structure SineOsc

Dans l'ensemble de ce projet, nous allons adopter une approche propre et organisé du code. Dans des projets C intégrant un grand nombre de fonctionnalités, une approche possible repose sur l'utilisation systématique de structures. Une structure va conserver l'ensemble des éléments relatifs à une fonctionnalité spécifique. Pour modifier les éléments de cette structure, nous allons ensuite définir et implémenter des fonctions spécifiques.

Définition de la structure

Pour centraliser les paramètres relatifs à la gestion de la sinusoide, une structure possible consiste à stocker les valeurs de l'amplitude, des termes $\cos (\phi )$ et $\sin (\phi )$, et des composantes directe et en quadrature.

src/audio_processor.h

typedef struct {
	float amp;  // Amplitude de la sinusoïde
    float incI; //terme cos(\varphi)
	float incQ; //terme sin(\varphi)
    float yI;   //composante directe
	float yQ;   //composante en quadrature
} SineOsc;

Manipulation 4

Ajoutez la définition de la structure SineOsc dans votre programme.

Fonctions associées

Pour gagner en modularité, nous allons ensuite définir et implémenter 3 fonctions permettant de manipuler la structure SineOsc. Par convention, le nom de ces fonctions débutera systématiquement par le nom de la structure associée. Pour l'ensemble de ces fonctions, nous utilisons un passage par adresse de la structure ce qui permet de simplifier la manipulation des paramètres.

src/audio_processor.h

void sineOscInit(SineOsc* osc, float amp, float yI, float yQ); //Initialisation du contenu de la structure
void sineOscSetInc(SineOsc* osc, float frequency);	//Changement des incréments à partir de la fréquence
float sineOscNextSample(SineOsc* osc); //Calcul de la nouvelle composante directe et en quadrature, puis calcul et renvoie du prochain échantillon.

Manipulation 5

Ajouter les définitions puis implémentez les fonctions sineOscInit, sineOscSetInc et sineOscNextSample. En utilisant la structure SineOsc, générez alors une sinusoïde de fréquence $f_0=220$ Hz et d'amplitude crête $a=0.9$.